|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
| ├ 2009年度 |
| ├ 2008年度 |
| ├ 2007年度 |
| ├ 2006年度 |
| ├ 2005年度 |
| ├ 2004年度 |
| ├ 2003年度 |
| ├ 写 真 |
| 中央アート出版社 TEL : 03-3561-7017 E-mail :info@chuoart.co.jp |

| MOON GATE by William L. Brian | |
| 第2章 月探査以前の月の引力 UFO Contactee No.84 1984より |
| アメリカの科学技術者ウィリアム・L・ブライアンの著書『ムーンゲート』は月の引力に関して驚くべき事実を暴露し、また月面の驚異的発見事をNASAが隠していることをあばいて、ジョージ・アダムスキーの体験記の内容が真実であったことを立証し、世界のUFO研究界に大きなショックを与えた。本号から原書の最初に返って第1章より逐次掲載する。この素晴らしい記事が読者に裨益(ひえき)すれば幸いである。 |
|
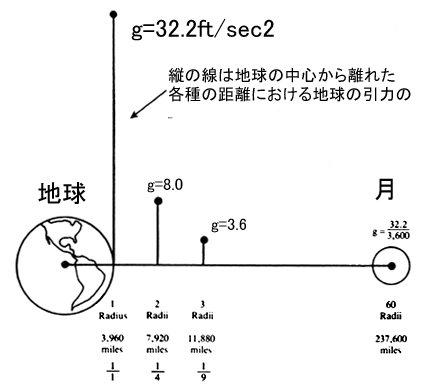
ニュートンの万有引力の法則とは 従来の科学によれば、月は地球の表面引力の6分の1しかないといわれていた。1666年にアイザック・ニュートン卿が万有引力の法則を公式化したが、それは上の結論を導き出したのである。この有名な法則によると、物体が他の物体に及ぼす引力は、2つの物体の質量の結果にかかっているという。したがって地球のような惑星はある力をもって他の物体を引っ張るのである。またこの法則は、惑星からの距離が大になるにつれて引力は減少するということになっている(訳注=正確に言えば、引力の大きさは2質点(物体)の質量の積に比例し、相互距離の2乗に反比例するという)。つまり宇宙空間において、地球または月から物体が遠ざかれば遠ざかるほど、それに及ぼす引力は弱まるのである。 ニュートンは、光の強さが光源から遠ざかるにしたがって弱まるのと同じぐあしに、地球の表面から引力も弱まってゆくことを発見した。光源から100フィートの位置にくらべて、200フィートの所にある一定の面にたいしてはわずか4分の1の程しか光があたらない。同様に、100フィートの位置にくらべて300フィート離れると、わずかに9分の1だけの量の光があたるにすぎない。この急速を減少は距離の2乗に反比例するという法則に従うからである。次の説明のために第1図を参照されたい。
地球の表面付近では、物体は毎秒32・2フィートの加速度で落下する。したがって1秒経過するごとに物体は毎秒32・2フィートずつスピードが増加する。そして加速を続けるけれども、いつかは空気の抵抗のために一定の速度に達する。 いま地球の表面から1人の観測者が遠ざかって行くとして、3960マイルの高度すなわち地球の中心から2倍の距離にあるとすると、光の例と同じように、地球の引力は4分の1に減少する。この距離になると体重は地球表面の重量の4分の1になるにすぎない。したがって200ポンドの人間はわずか50ポンドになる。しかもその人は地表のそれの4分の1すなわち秒速8フィートで加速されるから、静止点から出発して一定の距離を落ちるのに2倍の時間を要することになる。 地球の中心から半径3倍の距離すなわち表面から7920マイル(図1では3Radiiの位置)の位置まで遠ざかると、地球の引力は地表のそれの9分の1に減少する。200ポンドの人間ならば、わずか22ボンドになる。1秒落下するごとに秒速3・6フィート速くなるだけだ。 月の距離になると、地球が及ぼす引力は地表のそれの3600分の1にすぎないことになる。したがって月は毎秒秒速3600分の32・2フィート速くなって落下するにすぎない。これがもしも27日かそこらで地球の周囲をゆっくりと回らなければ、まもなく地球に撃突するだろう。この軌道すなわち回転が落下を防いでいるのである(訳注=地球を周回する月や人工衛星は、厳密に言えば落下しているのである)。人工衛星は月と同じように地球をまわる軌道に乗っている。しかし人工衛星は通常月よりも地球にうんと近いために、地球の引力はもっと強く働いており、人工衛星も軌道を周回するのにうんと速く進行する必要があるのだ。月は地球のまわりを時速2300マイルで進行するが、地球上空100マイルの位置にある人工衛星は、時速約17500マイルで飛ばねばならない。 ニュートンの引力の分析は軌道を回る月や地面に落下する物体などの観察によって考え出されたものだが、月のような天体に関して似たような実験が行われるまでは、表面引力の正しい価は決められない。ニュートンは月が他の天体に及ぼす月の引力を予報するのに、月の質量までも決定することはできなかった。その質量は後になって地球のそれの約82分の1と計算されたが、これは地球が地球と月の回転の共通中心部のまわりなどれだけ進行しているかを観測した結果である。こうして導き出された月の質量と地球の予報された質量が、月の表面引力を計算するのに応用されて、その結果地球のそれの6分の1となったのである。月は地球よりもうんと小さな天体なので、それに応じてより小さを表面引力を持っているはずだということは、科学者にとって不合理だとは思えなかったのだ。 平衡点のナゾ 宇宙船が地球を発進して月の引力の優勢範囲内に入ろうとする地点は、判断点(ニュートラル・ポイント)と呼ばれる。そこは地球の引力が月の引力と等しくなる位置である。月は地球よりも小さく、表面引力も小さいと思われてい薄ので、平衡点はかなり月に近い所になるはずだ。
たしかに月は地球の引力の6分の1だと考えられるとすれば、平衡点は地球と月のあいだの距離の約10分の9の位置になると計算される。月までの平均距離は約239000マイルであるから、そうすると平衡点は月の中心から約23900マイルの位置になる。第2図は平衡点を示す。この平衡点の距離は長いあいだ宇宙飛行関係科学者や技術者によって何度も予告され計算されてきたということを示すために、一連の参考資料を掲げることにしよう。 1965年に善かれた『宇宙飛行の原理』という本で、イギリス惑星間協会のメンバーであるM・バートレットは、次のようを平衡点の計算結果を出した。 「地球(の表面)から346000km、月(の表面)から38000kmの距離において、いわゆる平衡点Nの位置で、地球の引力と月の引力は等しくなる」 天文学者フランクリン・M・ブランレーが1966年に書いた『月の探険』の中で、平衡点は月から20000マイル、地球からは352000kmと出ている。 1969年にUSニューズ・アンド・ワールド・レポートによって書かれた、『月面のアメリカ』には、またもニュートラルポイントが月の表面から22000マイルと示されている。 1965年に書かれた『宇宙探険の数学』には、マール・H・アーレントがニュートンの引力の法則を応用し、月の質量を地球の質量の83分の1とあらわして、平衡点を計算した。月から地球までの距離を239000マイルと推定した彼の結論は次のとおりである。 「平衡点は月から23900マイルで、月までの距離のほぼ正確に10分の9の位置である」 別な23800マイル説が、1967年に『天体力学、ロケット、人工衛星、宇宙飛行』と題する著書でジョン・A・アイシールによって出された。彼は月までの距離を238,857マイルというすさまじい数字で表示して、月の質量と地球の割合を81・56とした。 1961年版のコリアー百科大辞典の『宇宙飛行』の項目には次のように述べてある。 「2つの引力の強さが等しくなり、互いに釣り合う位置があるはずで、この位置は月の表面から約23500マイルの所にある」 1960年版のエンサイクロピーディア・ブリタニカには、『惑星間探険』の項目に次のように述べてある。 「地球と月のあいだのいわゆる"平衡点"について。これは地球と月を結ぶ軸上の仮空のステーションであり(月から約19月レイディアイある)、そのむこう側の月の引力は地球のそれよりも強い」 19月レイディアイは月から20520マイルに等しい。 ここで読者にとって明らかになると思われるのは、こうした数値のあいだにはわずかを差が存在するという事実である。これは地球から月までの距離の推測がわずかに異なるのと、地球対月の質量の割合などのためである。この平衡点までの距離がどんなに異なるかを、地球から月までの距離にしたがって分析すると、次に示すような結果になる。各距離は地球の中心から月の中心までが測定されたものとしてある。
いずれにせよ、平衡点から月の中心までの距離は、22078マイルから25193マイルのあいだになるが、これは月が地球の表面引力の6分の1の引力を持つと仮定してのことである。 真の平衡点は隠されている これまでにきわめて多数の人や団体などが、さほどの大きな差なしに平衡点距離を述べてきているので、平衡点の位置に関しては疑問の余地はないように見える。技術的な素養のある読者を満足させるために、上に示した平衡点の距離の完全な値は本書の付録Aに掲げてある。 ここで読者は思い出すだろう。右の平衡点の距離はニュートンの万有引力の法則に基づいているということをー。加うるに上の数値を出した人達のほとんどは、平衡点の本当の位置に関する宇宙開発の発見について、たぶん気づいていなかったのだ。以前にも述べたように、月の近辺で落下しているか軌道を周回している物体を観測することによってのみ、実際の平衡点の距離が出せるし、月の本当の引力もきまるのだ。 この(観測による)情報は、1959年にさかのぼる最初の月探査機によってNASAまたはソ連に入手できたであろう。もし月探査機が1969年に先立ってうまく軌道に乗り、着陸していたとすれば、実際の平衡点距離は大衆にわかっているはずである。それが公開されたなら、月の表面引力を計算する正確な方法があることになる。 前に掲げた20000ないし25000マイルの距離よりも大きな平衡点距離の発見網がいまや考えられるだろう。引力というものは地球から遠ざかるにしたがって弱くなってゆくことをすでに説明した。月は地球と同じ状況を示す。したがって、月の表面から1080マイルの位置の月の引力は(月の中心から2レイディアイの距離)、表面引力の4分の1となる。同様にして、月の表面から2160マイル、すなわち3レイディアイの位置では表面引力の9分の1となる。 この考え方を心中に保つと、もし月の表面からの本当の平衡点距離が25000マイルよりもかなり大であるとすれば、月の表面引力は地球の表面引力の6分の1だという数値よりもはるかに大にならねばならないことになる。このことはニュートンの万有引力の法則は惑星ほどの大きさの天体までも含まないことを意味する。またこれはNASAと軍部が月の引力の本当の性質に関する情報を隠してしまったことをも意味するのだ。宇宙飛行士が月に安全に着陸しようとすれば、たしかにこの平衡点距離は正確に決定されねばならなかったのだ。これは実験によってこそ決定され得るものである。この発見の経緯については次章で述べることにしよう。 |
|
|
Copyright(C) 1999-2006 Ga Site All rights reserved.